When the population distribution is binomial with p = .5, how do the various sample sizes (i.e., N = 5, 25, or 100) affect the distribution of possible sample means?
As the Central Limit Theorem states, the sampling distributions for the different sample sizes each have a mean of .5, the population mean. Therefore, with a binomial population distribution and p = .5, sample size does not affect the accuracy of sample means.
Sorry, this answer is incorrect!
You answered that because the sampling distribution of the mean is centered around the population mean of .5 regardless of sample size, sample size does not affect the accuracy of sample means. Although the sampling distribution has a mean equal to the population mean, the Central Limit Theorem also states how the sample size affects the shape and spread of the sampling distribution. How so?
When N is 25 or smaller, the sampling distribution of the mean is noticeably skewed even with a binomial population distribution and p = .5.
Sorry, this answer is incorrect!
You answered that when N is 25 or smaller with p = .5, the sampling distribution of the mean is noticeably skewed. Actually when p=.5, the population is a symmetrical distribution. In this case, the sampling distributions of means for the various sample sizes are all exactly symmetrical around the mean of p = .5.
What is affected by sample size in this case is the continuity of the sampling distribution, with smaller samples producing a more limited and discrete set of possible means. If the population distribution was skewed (e.g., p = .1 as we will see next), even larger samples would be needed to produce a sampling distribution of the mean that approached being continuous and normal.
The sampling distribution based on N = 100 has sample means more tightly clustered around the mean of .5 and thus, yields more accurate estimates of the population mean than the smaller sample sizes.
Yes, good answer!
The sampling distribution based on N = 100 produces more accurate sample means than when N = 5 or N =25 for both normal populations and binomial populations with p = .5. In other words, sample means become less variable with larger sample sizes. This may be seen mathematically in the formula for the standard error of the mean:
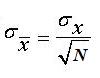
Regardless of sample size, the sampling distribution of the mean tends to be binomial, just like the parent population.
Sorry, this answer is incorrect!
You answered that regardless of sample size, the sampling distribution of the mean will tend to resemble the parent distribution which is binomial. Whereas the only possible outcomes in the parent population are 0 and 1, the sample means for the various sample sizes include values between 0 and 1.
![]()

