Power Exercise 1b: Power and Mean Differences (Small Effect)

Now we will assess the power of a test for a rival training program, the DEUCE program. The mean score for the population of graduates of this program is 520. Again we assume the population distribution is normal with a standard deviation of 100. Using the formula for d, we find that the population effect size for the DEUCE program is only .20.

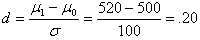
Recall the effect size for the ACE program was much larger:

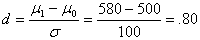
1b. Before drawing samples, consider how the statistical power will differ for a test of DEUCE graduates compared to the power we found for a test of ACE graduates. That is, do you expect you will be more likely or less likely to reject the null hypotheses for a sample of 25 graduates drawn from the DEUCE program compared to a similar test for the ACE program?

I predict that statistical power for the test of the DEUCE program compared to the test of the ACE program will be:

Less

Correct! All else being equal, the test for the program with the larger effect size will have greater statistical power, so the test of the DEUCE program will have LESS power than the test of the ACE program..

The Same

Try again.

Greater

Try again.

With the applet you will be able to change the effect size and watch what happens to statistical power. Your goal for this exercise is to be able to explain to a friend why statistical power is greater when the effect size is greater.

To simulate drawing a sample of 25 from graduates from the DEUCE program, enter the following information into the WISE Power Applet:

  • μ0 = 500 (null mean);
  • μ1 = 520 (alternative mean);
  • σ = 100 (standard deviation);
  • α = .05 (alpha error rate, one tailed);
  • n = 25 (sample size).
    •

    Press enter/return after placing the new values in the appropriate boxes!

    Do three simulations of drawing a sample of 25 cases, and record the results below.

    Trial 1 2 3 4 5 6 7 8 9 10
    Mean 509 511 513 502 492 513 533
    Z-Score 0.45 0.55 0.65 0.10 -0.40 0.65 1.65

    1c. What is the power for this test as shown in the applet?

    1d. How many of your ten simulated samples allowed you to reject the null hypothesis?
    (Use one-tailed alpha α = .05, z = 1.645, so reject H0 if your z-score is greater than 1.645)

    1e. For the ACE program, the effect size was .8 and the power of the statistical test was .991; what can you conclude about the relationship between effect size and power?

    A. The test for the ACE program, which had a larger effect size, had more power.

    Correct! The test of the ACE program has more power because ACE has a larger effect size. As the magnitude of the difference between the means of the null and alternative population sampling distribution increases with respect to their standard deviation (as the null and alternative sampling distributions overlap to a lesser extent), the less likely it is that a randomly sampled mean from the alternative population will be mistaken for a sample mean taken from the null distribution.

    B. The test for the DEUCE program, which had a smaller effect size, had more power.

    Incorrect. Smaller effect sizes are associated with less power. The DEUCE program has a smaller effect size, which indicates that the null and alternative distributions overlap to a greater extent compared to the ACE program. Consequently, it is more likely that a randomly sampled mean from the DEUCE program will be mistaken to have come from the null distribution compared to a randomly sampled mean taken from the ACE population.

    C. Effect size is unrelated to power.

    Incorrect. If nothing else changes, power increases as effect size increases. As the effect size increases the sampling distributions overlap to a lesser extent and it is less likely that a randomly sampled mean taken from the alternative distribution will be mistaken for a mean from the null distribution

    Next

    Loading