Recall from the Central Limit Theorem that the standard error of the mean is equal to the population standard deviation, s , divided by the square root of the sample size:
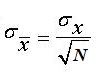
Thus, for a sample of N = 5 and population standard deviation of s = 100, the standard error of the mean is 100/2.236 or 44.721.
We know that approximately 95% of scores in a normal distribution are within two standard deviations of the mean (1.96 standard deviations, to be more precise). If the sampling distribution of means is normal, then we expect about 95% of means from samples with N = 5 to be within about 88 points of the actual population mean (1.96 * 44.721 = 87.653), from about 412 to 588 (see figure below).
![]()

