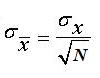How closely do sample means cluster around the population mean? The standard deviation the distribution of all possible sample means for samples of size Nis called the “standard error of the mean” (or “standard error”). Recall from the Central Limit Theorem that the standard error, s x, is equal to the population standard deviation, s x, divided by the square root of the sample size, N:
Thus, for a sample of N = 25 and population standard deviation of s x = 100, the standard error of the mean is 100/5 or 20. For a sample of N = 100 and population standard deviation of s x = 100, the standard error of the mean is 100/10 or 10. Notice that when sample size N is increased, the standard error becomes smaller. In our example, by quadrupling the sample size, the standard error was cut in half.
![]()