You may now briefly review the Central Limit Theorem or continue on below.
Our researcher friend plans to draw a sample of 100 people to take the Life Satisfaction scale. To simulate this in the applet, select the following options: Normal(Mu=500; Sigma=100), N=100, Show sample data (uncheck all other ‘show’ options for now). If you have questions about any of the options, please consult the instructions for using the applet.
Click on Draw a sample, and enter the value displayed for Last mean = in the first space below. Then click on Draw a sample nine more times and record each mean below.
How many of your 10 sample means fell outside of the range 470 to 530?
Click on Show obtained means to see a display of all ten means.
Notice how tightly clustered the obtained means are compared to the individual scores.
Click Draw 100 samples to see the means for 100 different samples, each of size N=100.
Click Show sampling distribution of the mean to see how closely the observed sample means match the actual distribution of all possible means for samples of size N=100.
Now in terms of their means and variability, describe in the box below how this sampling distribution of the mean for N=100 compares to the distribution of scores in the population (click Show population).
Q2. What is the probability that a randomly selected sample of N=100 American adults has a mean Life Satisfaction score within 30 points of the population mean (i.e., between 470 and 530)?
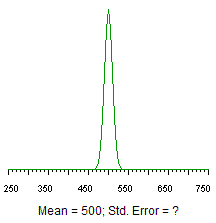
Figure 2. Sampling distribution of the mean for the Life Satisfaction Scale, N=100.
First, make a rough estimate of the answer using Figure 2.
You can also estimate the answer by counting the number of sample means out of 100 that fall within the range 470 to 530. It may be easier to see if you turn off Show sampling distribution of the mean. You don’t need to get an exact count, but we see that when we draw a sample with N=100, it is unlikely that the sample mean is in error by more than 30 points as an estimate of the mean Life Satisfaction for the population (i.e., it is unlikely to find a sample mean that deviates as much as 30 points from the mean). Were any of your 100 sample means 30 or more points away from the population mean?
Now solve for the exact answer. You may use a table of probabilities for the standardized normal distribution or use the p–z converter to convert from a z-score to probability.
Show A Hint
We know that the possible means are normally distributed with a mean of 500. If we can find the standard deviation of this distribution, we can find the z score corresponding to 530, and then use the z table or p–z converter to find the probability of observing a sample mean between 500 and 530, and between 500 and 470.
Show Another Hint
According to the CLT, the standard deviation of the mean (also called the standard error) is equal to the population standard deviation, 100, divided by the square root of the sample size, also 100. Thus, the standard error = 100/ (square root of 100) = 100/10 = 10. Using this standard error of 10, you can now convert 470 and 530 (scores that deviate from the mean by 30) into z scores and find their corresponding probabilities.
The answer is over 99%. The exact answer and detailed calculations are in the answer section.
![]()

