We saw that the standard deviation of the sampling distribution is smaller when the sample size is larger. The Central Limit Theorem gives us an exact formula. The standard deviation of the sampling distribution of means equals the standard deviation of the population divided by the square root of the sample size. The standard deviation of the sampling distribution is called the “standard error of the mean.”
The formula for the standard error of the mean, sx̄, is
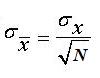 , where sx̄is the standard deviation of the population and Nis the sample size.
, where sx̄is the standard deviation of the population and Nis the sample size.
We can use this formula to calculate the standard error of any sampling distribution if we know the sample size and the population standard deviation.
Imagine you draw a sample of 100 cases from a population with a mean of 57 and a standard deviation of 20.
What are the mean mx̄ and the standard error sx̄ for the sampling distribution?
m = 57, s = 20
Sorry, this answer is incorrect!
Your answer describes the population, not the sampling distribution. Remember that the Central Limit Theorem states that for a given population and sample size:
The sampling distribution has the same mean as the underlying population, but a smaller standard deviation.
Notice how the sample size N is used in the formula, and then recalculate your answer.
m = 57, s = 200
Close, but not correct!
You seem to have the right idea, but you may have made a math error. Check the formula for the standard error of the mean. Be careful with decimal points.
m = 57, s = 4
Close, but not correct!
You seem to have the right idea, but you may have made a math error. Check the formula for the standard error of the mean. Did you remember to take the square root?
m = 57, s = 2
Yes, excellent!
The sampling distribution has less variance and is narrower with larger sample sizes. We divide the population standard deviation, sx, by the square root of the sample size, N, to get the standard error of the mean sx̄
![]()

