Calculate the approximate proportion of Ourtown women who are 5 feet, 7 inches (i.e., 67 inches) tall or taller.
Recall that the height of women in Ourtown is approximately normally distributed with a mean of 5 feet, 4 inches (i.e., 64 inches) and a standard deviation of 3 inches. You may consult a z-table or the p-z converter.
Which answer is correct?
0%
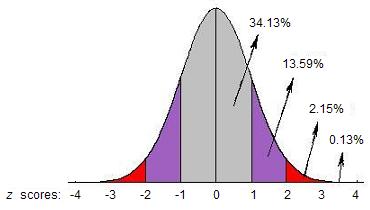
Sorry, this answer is incorrect! Because the distribution is normal, we can use z scores to find probabilities. What is the z-score corresponding to someone who is 67 inches tall in a population with a mean of 5 feet, 4 inches and a standard deviation of 3 inches? Convert 67 inches to a z-score and mark this value on the normal distribution below. We can see that some women in Ourtown are 5 feet, 7 inches (67 inches) tall or taller; therefore 0% could not be a correct answer.
2%
Sorry, this answer is incorrect! Because the distribution is normal, we can use z scores to find probabilities. What is the z-score corresponding to someone who is 67 inches tall in a population with a mean of 5 feet, 4 inches and a standard deviation of 3 inches? Convert 67 inches to a z-score and mark this value on the normal distribution below. We can see that some women in Ourtown are 5 feet, 7 inches (67 inches) tall or taller; therefore 0% could not be a correct answer.

14%
Sorry, this answer is incorrect! You may have forgotten to include women who are taller than 5 feet, 10 inches (70 inches). Look at the area under the normal curve shown below. Where would the value 5 feet, 7 inches fall under the normal curve? Your answer is the proportion of women who are between 5 feet, 7 inches and 5 feet, 10 inches tall. What proportion of the area under the curve falls to the right of 5 feet, 7 inches?

16%
Correct! The z-score that corresponds to 5 feet, 7 inches is +1.00. The proportion of the area under the normal curve that falls beyond this z-score is .1587 or approximately 16% of the population. GREAT WORK!
Show me a hint
The question asks what proportion of women are 5 feet, 7 inches (67 inches) tall or taller. We need to standardize the height and be confident that the distribution is normal in shape to be able to use the z-table or the p–z converter to translate from a z-score to a probability. To find the z-score corresponding to a height of 67 inches, use the formula, where x is the raw score, m is the mean, and s is the standard deviation:
![]()
Here x = 67 inches, m = 64 inches, and s = 3 inches. See the review of z scores for more information.
![]()

