Researchers argue that traditional hypothesis testing based on arbitrary alpha values is not particularly useful in describing statistical relationships. Amongst the most useful statistics available is the confidence interval. For the independent samples t-test we can determine an estimate, based on the data found in our samples, that has a high probability (usually set at 95 or 99 %) of encompassing the true populations values of the differences between the means.
The formula for the calculation of this value is: ![]() Where the t value corresponds to the critical rejection values for a .05 two tailed test. Note: if using alpha = .01, we use a t .005 value. The t value is half of the alpha as we are constructing an estimate of the upper and lower limits of the intervals at each tail of the distribution.
Where the t value corresponds to the critical rejection values for a .05 two tailed test. Note: if using alpha = .01, we use a t .005 value. The t value is half of the alpha as we are constructing an estimate of the upper and lower limits of the intervals at each tail of the distribution.
Several arguments exist for the use of confidence intervals exist. The fundamental advantage of confidence intervals is the range of values obtained allow us to both test a hypotheses and get descriptive information regarding the relationship. For our CI, if the computed value does not include the values hypothesized in the null (difference between means is 0), then we can reject our null hypothesis. However, beyond the simple dichotomous rejection of hypotheses, we are also given descriptive information regarding the range of probable value for the “true” differences between the two means. Thus, CI’s can tell us not only whether there are differences between Belize and Samoa but, also can answer the question “how large are the differences?”
Calculation Example
The formula for the calculation of this value is: ![]()
For our calculation we need the following values:
![]() and
and ![]() and
and ![]()
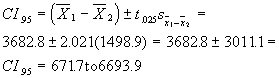
This yields a range of values which have a 95% probabilty of encompassing the “true” differences between ![]() in the population.
in the population.
Application Example
For our confidence interval: CI.95 = ![]() = 671.7 to 6693.9
= 671.7 to 6693.9
This is interpreted as follows: there is a 95% probability that the interval 671.7 to 6693.9 includes the true difference between ![]() . Because our CI does not encompass zero, the value in the null hypothesis, we can reject the null hypothesis that the mean difference between Belize and Samoa is zero. More importantly, in addition to the information given by the hypothesis test, we are given a range in which we believe the true population value exists. Thus we can answer both the following questions:
. Because our CI does not encompass zero, the value in the null hypothesis, we can reject the null hypothesis that the mean difference between Belize and Samoa is zero. More importantly, in addition to the information given by the hypothesis test, we are given a range in which we believe the true population value exists. Thus we can answer both the following questions:
1. Are the groups different? Yes (the CI does not encompass 0)
2. How different? Likely somewhere between 671 and 6694 feet.
![]()

