As the effect size increases, the power of a statistical test increases. The effect size, d, is defined as the number of standard deviations between the null mean and the alternate mean. Symbolically,
where d is the effect size, μ0 is the population mean for the null distribution, μ1 is the population mean for the alternative distribution, and σ is the standard deviation for both the null and alternative distributions. From the equation it can be noted that two factors impact the effect size: 1) the difference between the null and alternative distribution means, and 2) the standard deviation. For any given population standard deviation, the greater the difference between the means of the null and alternative distributions, the greater the power. Further, for any given difference in means, power is greater if the standard deviation is smaller. In the following exercise, we will use the power applet to explore how the effect size influences power. Your task is to find a good way to explain how this works to a friend.
Click here for more information on effect sizes.
Exercise 1a: Power and Mean Differences (Large Effect)
How probable is it that a sample of graduates from the ACE training program will provide convincing statistical evidence that ACE graduates perform better than non-graduates on the standardized Verbal Ability and Skills Test (VAST)? How likely is it that a rival competitor, the DEUCE training program, will provide convincing evidence? Power analysis will allow us to answer these questions.
We will use the WISE Power Applet to examine and compare the statistical power of our tests to detect the claims of the ACE and DEUCE training programs. We begin with a test of ACE graduates.
We assume that for the population of non-graduates of a training course, the mean on VAST is 500 with a standard deviation of 100. For the population of ACE graduates the mean is 580 and the standard deviation is 100. Symbolically, μ0 = 500, μ1 = 580, and σ = 100. Both distributions are assumed to be normal.
How large is the effect size? The formula for d shown below indicates that the effect size for the ACE program is .80. This tells us that the mean for the alternative population is .80 standard deviations greater than the mean for the null population.
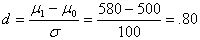
The z-score of a sample mean computed on the null sampling distribution allows us to determine the probability of observing a sample mean this large or larger if the null hypothesis is true.
To prepare the simulation, enter the following information into the applet below:
Press enter/return after placing the new values in the appropriate boxes!
To simulate drawing one sample of 25 cases, press Sample. The mean and z-score are shown in the applet (bottom right box). (Remind me what a z-score is). Record these values in the first pair of boxes below (you may round the mean to a whole number).
| Trial | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 579 | 574 | 594 | 600 | 541 | 585 | 578 | |||
| Z-Score | 3.96 | 3.72 | 4.69 | 4.99 | 2.04 | 4.23 | 3.92 |
Is this sample mean large enough to allow you to reject the null hypothesis? How likely is it that you would observe a sample this large or larger if the null hypothesis was true so that you really were sampling from the blue distribution? (Answer: The p-value is the probability of observing a mean as large or larger than your sample mean if the null hypothesis is true.)
Now draw two more samples and record the mean and z for each in the boxes. These values will be saved and used later and can be printed for a homework exercise. Some of the boxes have already been filled out for you.
The power of this statistical test is the probability that the mean of a random sample of size n will be large enough to allow us to correctly reject the null hypothesis. Because we are actually sampling from the Alternative Population (red distribution), the probability that we will observe a sample mean large enough to reject H0 corresponds to the proportion of the red sampling distribution that is to the right of the dashed line. For this example, we can use the value provided by the applet, .991. (Click here to see calculations of power.)
Thus, if we draw a sample of 25 cases from ACE graduates, the probability is 99.1% that our sample mean will be large enough that we can reject the null hypothesis that the sample came from a population with a mean of only 500. The probability that we will fail to reject H0 is only 1.000 – .991 = .009, less than one chance in 100.
1a. How many times could you reject the null hypothesis in your ten samples?
(With one-tailed alpha α = .05, z = 1.645, so reject H0 if your z-score is greater than 1.645)
![]()

